Recopilación de vídeos de trazados relacionados con la circunferencia, como divisiones en partes iguales y métodos de rectificación.
Índice de Contenidos
- 1 Trazado básico de circunferencia.
- 2 División de la circunferencia.
- 2.1 Dividir una circunferencia en 2 partes iguales.
- 2.2 Dividir una circunferencia en 3 partes iguales.
- 2.3 Dividir una circunferencia en 4 partes iguales.
- 2.4 Dividir una circunferencia en 5 partes iguales.
- 2.5 Dividir una circunferencia en 6 partes iguales.
- 2.6 Dividir una circunferencia en 7 partes iguales.
- 2.7 Dividir una circunferencia en 8 partes iguales.
- 2.8 Dividir una circunferencia en 10 partes iguales.
- 2.9 Dividir una circunferencia en 12 partes iguales.
- 2.10 Dividir una circunferencia en 14 partes iguales.
- 2.11 Dividir una circunferencia en 15 partes iguales.
- 3 Rectificación de circunferencia.
- 3.1 Rectificación de una circunferencia por el método de Arquímedes.
- 3.2 Rectificación de una circunferencia por el método de Specht.
- 3.3 Rectificación de una semicircunferencia por el método Kochanski.
- 3.4 Rectificación de un cuadrante de circunferencia por el método Mascheroni.
- 3.5 Rectificación de un arco menor de 90 grados.
- 4 Apuntes básicos sobre circunferencias.
- 4.1 Definición y elementos de una circunferencia.
- 4.2 Diferencia entre círculo y circunferencia.
- 4.3 Posiciones relativas entre un punto y una circunferencia.
- 4.4 Posiciones relativas entre una circunferencia y una recta.
- 4.5 Posiciones relativas entre dos circunferencias.
- 4.6 Teoremas relativos a la circunferencia y al círculo.
- 4.7 Ángulos de la circunferencia y potencia.
Trazado básico de circunferencia.
Trazar la circunferencia que pasa por tres puntos.
Hallar el centro de una circunferencia.
División de la circunferencia.
Dividir una circunferencia en 2 partes iguales.
Dividir una circunferencia en 3 partes iguales.
Dividir una circunferencia en 4 partes iguales.
Dividir una circunferencia en 5 partes iguales.
Dividir una circunferencia en 6 partes iguales.
Dividir una circunferencia en 7 partes iguales.
Dividir una circunferencia en 8 partes iguales.
Dividir una circunferencia en 10 partes iguales.
Dividir una circunferencia en 12 partes iguales.
Dividir una circunferencia en 14 partes iguales.
Dividir una circunferencia en 15 partes iguales.
Rectificación de circunferencia.
Rectificación de una circunferencia por el método de Arquímedes.
Rectificación de una circunferencia por el método de Specht.
Rectificación de una semicircunferencia por el método Kochanski.
Rectificación de un cuadrante de circunferencia por el método Mascheroni.
Rectificación de un arco menor de 90 grados.
Apuntes básicos sobre circunferencias.
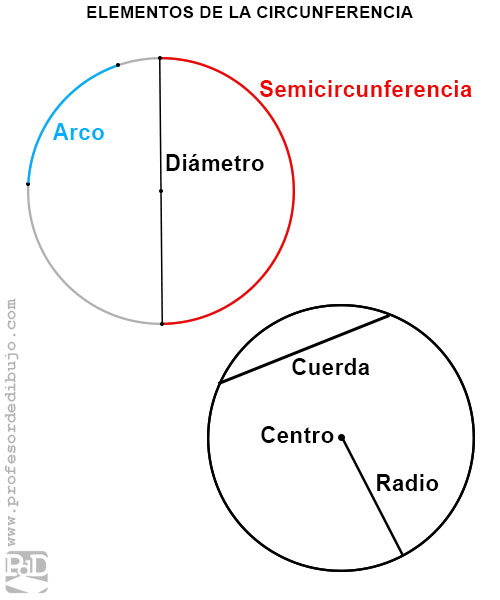
Definición y elementos de una circunferencia.
La circunferencia es una línea curva cerrada, cuyos puntos equidistan de otro punto llamado centro.
Los principales elementos de una circunferencia son:
- Arco: porción de la circunferencia comprendida entre dos de sus puntos.
- Centro: punto desde el que se sitúan a igual distancia todos los puntos de la circunferencia.
- Radio: segmento situado entre el centro de la circunferencia y cualquier punto de esta.
- Cuerda: Segmento que une dos puntos de una circunferencia. Divide a la circunferencia en dos arcos. La mayor cuerda de una circunferencia sería el diámetro.
- Diámetro: segmento delimitado por dos puntos de una circunferencia y que pasa por el centro. Su medida sería dos veces la del radio. El diámetro divide la circunferencia en dos partes iguales llamadas semicircunferencias.
- Semicircunferencia: arco comprendido por media circunferencia.
Diferencia entre círculo y circunferencia.
El círculo es la porción del plano delimitada por una circunferencia.
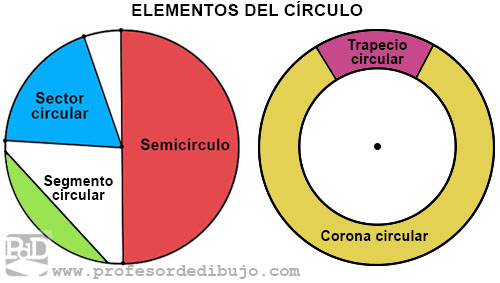
Elementos del círculo:
- Semicírculo: sería la porción que delimita medio círculo. Un diámetro divide al círculo en dos semicírculos.
- Sector circular: es la porción del círculo delimitada por dos radios.
- Corona circular: es la porción de un circulo resultante de restarle otro círculo menor concéntrico.
- Trapecio circular: es la porción de corona circular delimitada por dos radios.
- Segmento circular: es la porción del circulo limitada entre una cuerda y el arco comprendido entre los extremos de la misma.
Posiciones relativas entre un punto y una circunferencia.
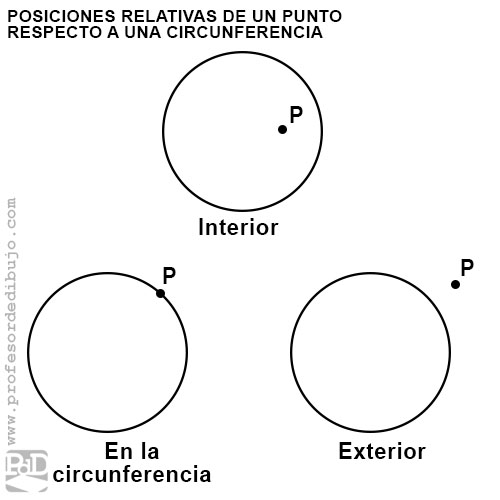
Según su posición, un punto puede estar respecto a una circunferencia:
- Interior: el punto está dentro de la circunferencia.
- En la circunferencia: el punto es uno de los puntos de la circunferencia.
- Exterior: el punto está fuera de la circunferencia.
Posiciones relativas entre una circunferencia y una recta.
Según su posición, una recta puede ser respecto a una circunferencia:
- Tangente: la recta tiene un único punto en común con la circunferencia y es perpendicular al radio que pasa por dicho punto.
- Secante: la recta corta a la circunferencia en dos puntos.
- Exterior: la recta no tiene punto en común con la circunferencia.

Posiciones relativas entre dos circunferencias.
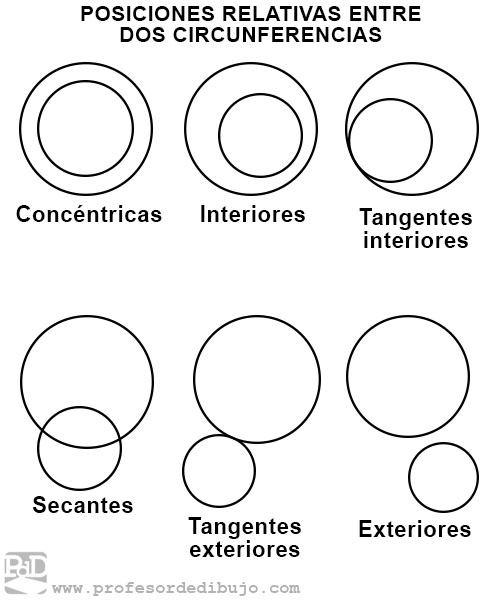
Según la posición que ocupan dos circunferencias pueden ser:
- Exteriores: las dos circunferencias no tienen punto en común.
- Tangentes exteriores: las dos circunferencias sólo tienen un punto en común y ninguna está dentro de la otra.
- Secantes: Las dos circunferencias se cortan en dos puntos.
- Tangentes interiores: las dos circunferencias sólo tienen un punto en común y una está dentro de la otra.
- Interiores: Una circunferencia está dentro de la otra, sin tener punto en común y sin compartir centro.
- Concéntricas: Una circunferencia está dentro de la otra y comparten el mismo centro.
Teoremas relativos a la circunferencia y al círculo.
Los conceptos relacionados a continuación ayudan a entender mejor la realización de futuros trazados geométricos.
- Por tres puntos no alineados sólo pasa una circunferencia.
- Todo diámetro divide a la circunferencia y al círculo en dos partes iguales: semicírculo o semicircunferencia.
- Los radios de una circunferencia o de circunferencias iguales son iguales entre sí.
- En una circunferencia o en circunferencia iguales se cumple que a ángulos centrales iguales les corresponde arcos iguales. Se cumple de modo reciproco, a arcos iguales le corresponden ángulos centrales iguales.
- En una circunferencia o circunferencias iguales se cumple que a cuerdas iguales les corresponde arcos iguales. También se cumple de modo reciproco.
- La mediatriz de la cuerda de una circunferencia siempre pasa por el centro de esta. por lo tanto, la mediatriz contiene un diámetro de la circunferencia.
- En una circunferencia, el diámetro o el radio perpendicular a una cuerda la biseca, es decir la divide en dos partes iguales. también biseca al angulo correspondiente a la cuerda.
- En una circunferencia o en circunferencias iguales, las cuerdas iguales equidistan del centro.
- Cuando una recta es secante la distancia que la separa del centro es menor al radio. Si se trata de una recta exterior la distancia será mayor que la del radio. En el caso de una recta tangente la distancia que la separa del centro de la circunferencia es la medida del radio.
- Del concepto anterior se deduce que por un punto de una circunferencia sólo pasa una recta tangente.
Ángulos de la circunferencia y potencia.
En este punto, te dejo enlaces a dos temas algo más complejos relacionados con las circunferencias, como pueden ser los ángulos de las circunferencias y una explicación básica de las potencias en dibujo técnico.
