Esta sección está dedicada a la proporcionalidad en la geometría. Encontrarás distintas explicaciones sobre relaciones proporcionales entre segmentos, tratando temas con el teorema de Tales y la proporción áurea entre segmentos.
Índice de Contenidos
- 1 Vídeos de proporcionalidad.
- 1.1 Cuarto proporcional a tres segmentos.
- 1.2 Tercero proporcional a dos segmentos.
- 1.3 Medio proporcional a dos segmentos.
- 1.4 Dividir un segmento en tres partes proporcionales a otros tres segmentos.
- 1.5 Dividir un segmento en partes iguales (aplicando teorema de Tales).
- 1.6 Dividir un segmento en media y extrema razón. División áurea de un segmento.
- 1.7 Trazar un segmento AC del cual sea áureo el segmento dado AB.
- 2 Apuntes de Proporcionalidad.
Vídeos de proporcionalidad.
Cuarto proporcional a tres segmentos.

Tercero proporcional a dos segmentos.

Medio proporcional a dos segmentos.

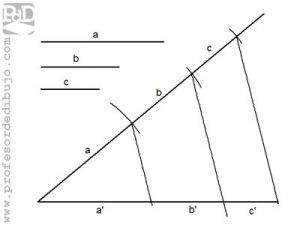
Dividir un segmento en tres partes proporcionales a otros tres segmentos.

Dividir un segmento en partes iguales (aplicando teorema de Tales).

Dividir un segmento en media y extrema razón. División áurea de un segmento.

Trazar un segmento AC del cual sea áureo el segmento dado AB.

Apuntes de Proporcionalidad.
Antes de hablar de proporcionalidad, sería conveniente repasar dos términos:
Forma: es la apariencia exterior de cualquier elemento y queda definida por un contorno que delimita los límites de su figura y una estructura que establece una relación entre las distintas partes que la componen.
Tamaño: es una cualidad de la forma que se refiere a su magnitud respecto a otras y al espacio. De modo que se trata de una cualidad relativa.
Dos figuras son proporcionales si la relación de medida entre las partes de una de ella se corresponde con la relación de las partes de la otra. De este modo, existe proporcionalidad entre figuras de igual forma y tamaño, pero también entre figuras de distinto tamaño pero idéntica forma.
También podemos entender la proporción como la relación existente entre las partes de una figura respecto a su totalidad.
Razón.
Para poder establecer una comparación entre dos magnitudes es necesario establecer un relación entre ellas. A esa relación se le llama razón y es el resultado de dividir una magnitud por la otra.
En este sentido, podemos considerar proporción como la igualdad entre dos razones. De este modo, si tenemos la siguiente proporción: a/b = c/d, decimos que a y d son los términos extremos de la proporción. Mientras que b y c son los términos medios.
Teorema de Tales.
El teorema de Tales afirmaba que si un haz de rectas paralelas cortan a dos rectas concurrentes (que se cortan en un punto) se generan una serie de segmentos en ambas rectas que son proporcionales.
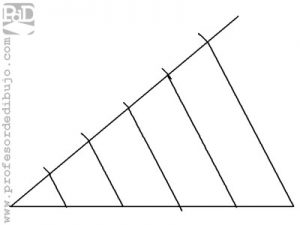
Podemos observar que las rectas s y r son dos rectas concurrentes, mientras que t, u, v y w son rectas paralelas entre ellas. Este haz de rectas paralelas cortan a las rectas r y s en una serie de puntos. Estos puntos determinan los segmentos a, b y c en la recta r. Mientras que en la recta s tenemos los segmentos d, e y f. Según el teorema de Tales podemos concluir que se cumple la siguiente proporción: a/d = b/e = c/f.
Basándonos en el teorema de Tales podemos realizar diversos trazados para obtener segmentos proporcionales a otros ya dados.
Cuarto proporcional a tres segmentos.
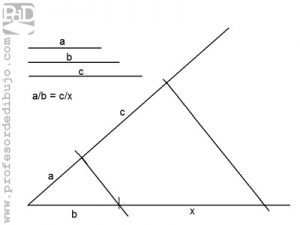
Teniendo tres segmentos a, b y c, el segmento cuarto proporcional, al que llamaremos x, será aquel que cumpla la siguiente proporción: a/b = c/x.
Vídeo: Hallar el cuarto proporcional a tres segmentos.
- Dibujamos una semirrecta r horizontal que parte desde un punto O.
- Partiendo desde ese mismo punto de origen dibujaremos otra semirrecta llamada s, con una inclinación cualquiera.
- Partiendo desde el punto O y sobre la recta r, transportaremos el segmento b.
- Igualmente, partiendo desde el punto O y sobre la recta s, transportaremos el segmento a y seguidamente el segmento c.
- Teniendo en cuenta que el punto O es uno de los extremos de los segmentos a y b, unimos con una recta el otro extremo del segmento a con el otro extremo del segmento b.
- A continuación trazamos una paralela a dicha recta que pase por el extremo del segmento c y que corte a ambas rectas r y s.
- El segmento resultante de la intersección de estas dos paralelas con la recta r es x.
Tercero proporcional a otros dos segmentos.
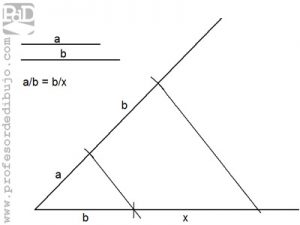
Debemos considerar la posibilidad de que los medios o los extremos sean iguales. En este caso tenemos el segmento a es un extremo, b es ambos medios y debemos hallar x de modo que se cumpla a/b = b/x.
Vídeo: Hallar el tercero proporcional a dos segmentos.
- Al igual que en el caso anterior, dibujamos dos semirrectas que partan desde un punto O, una horizontal y otra inclinada.
- Sobre la recta inclinada y partiendo desde O transportamos el segmento a.
- Ahora transportamos el segmento b a ambas rectas. En la horizontal partiendo desde O y en la recta inclinada partiendo desde el extremo del segmento a.
- A continuación unimos el extremo del segmento a con el extremo del segmento b situado en la recta horizontal.
- Para terminar, trazamos una paralela a la resta anterior que pase por el extremo del segmento b situado en la recta inclinada.
- De este modo obtenemos x en la recta horizontal. Sería el segmento que parte del extremo de b hasta el punto de corte de la paralela que hemos trazado.
Medio proporcional de otros dos segmentos.
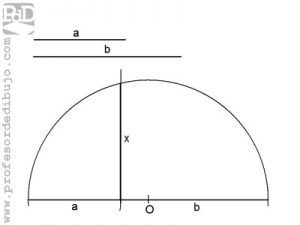
En este caso queremos hallar ambos medios que son iguales de mos que se cumpla la proporción a/x = x/b. Dicho de otro modo a por b es igual a x al cuadrado.
Para ello vamos a considera el teorema de la altura de Euclides que afirma que en un triángulo rectángulo la altura de la hipotenusa es la media proporcional de los dos segmentos en los que divide a la hipotenusa.
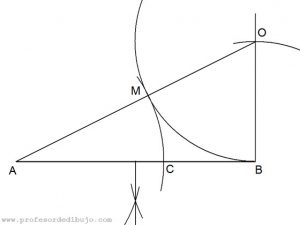
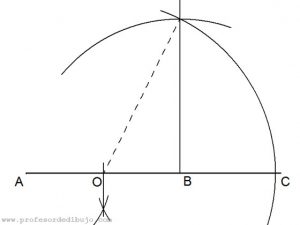
Para hallar el segmento medio proporcional de a y b seguiremos los siguientes pasos:
- En una semirrecta sumamos ambos segmentos.
- Hallamos el punto medio O del segmento resultante.
- Desde O hacemos centro con el compás y trazamos una semicircunferencia con el radio hasta cualquiera de los extremos del segmento resultante de la suma de los segmentos a y b.
- Trazamos una perpendicular a dicho segmento por el punto de unión de los segmentos a y b hasta cortar el arco trazado.
- El segmento obtenido es la media proporcional de a y b.
División de un segmento en partes iguales.
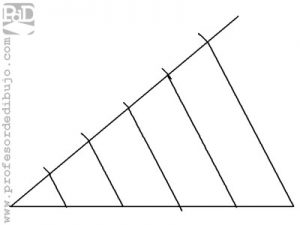
Para dividir un segmento en un número determinado de partes iguales aplicaremos los principios del teorema de Tales.
Los pasos a seguir serán los siguientes:
- Tomaremos uno de los extremos del segmento que queremos dividir como punto O
- Desde el punto O alzamos una semirrecta con una inclinación cualquiera.
- En dicha semirrecta y partiendo desde O colocaremos una medida cualquiera tantas veces como divisiones deseemos del segmento.
- Trazaremos una recta que una el extremo de la última de estas medidas con el extremo del segmento a dividir.
- Por el resto de marcas trazaremos paralelas a la recta anterior.