Curvas Cónicas

Vídeos didácticos sobre curvas cónicas desde el enfoque del dibujo técnico. Trazados de elipses, determinación de tangentes y algunos aspectos teóricos.

Elipse

Trazado de elipses.

1. Trazar una elipse conocidos sus ejes, método de localización de puntos.

   ---

2. Trazar una elipse conocidos sus ejes, método de intersección de rectas.

   ---

3. Trazar una elipse conocidos sus ejes, método de afinidad (proyección de puntos).

   ---

4. Trazar una elipse conocidos dos diámetros conjugados.

   ---

Determinar elemnentos de la Elipse.

1. Determinar los ejes de una elipse dada.

   ---

Tangencias a una elipse.

1. Tangente a una elipse por un punto de la curva, método de la circunferencia focal.

   ---

2. Tangente a una elipse por un punto de la curva, método de la circunferencia principal.

   ---

3. Tangente a una elipse por un punto exterior, método de la circunferencia focal.

   ---

4. Tangente a una elipse por un punto exterior, método de la circunferencia principal.

   ---

Parábola

Trazado de Parábolas.

1. Trazado de una parábola localizando puntos por radios vectores.

   ---

Tangencias de la Parábola.

Tangente a una parábola por un punto de la curva.

Tangente a una parábola paralela a una dirección dada por un vector.

Tangentes a una parábola pasando por un punto exterior.

Hipérbola.

Trazado de una Hipérbola.

Trazado de una hipérbola localizando puntos por radios vectores.

Tangencias de la Hipérbola.

Tangente a una hipérbola por un punto de la curva.

Método de los radios vectores.

Método de la circunferencia focal.

Tangente a una hipérbola paralela a una dirección dada por un vector.

Tangentes a una hipérbola pasando por un punto exterior.

Trazar las asíntotas de una hipérbola dados los focos y el eje real.

Conceptos básicos sobre curvas cónicas.

Cuando una recta (generatriz) gira en torno a otra recta (eje) a la que corta se genera un cono.

Se denominan curvas cónicas al conjunto de curvas resultantes de la intersección de un plano con la superficie cónica de revolución. La inclinación de dicho plano respecto al eje de la superficie cónica determina el tipo de curva obtenida.

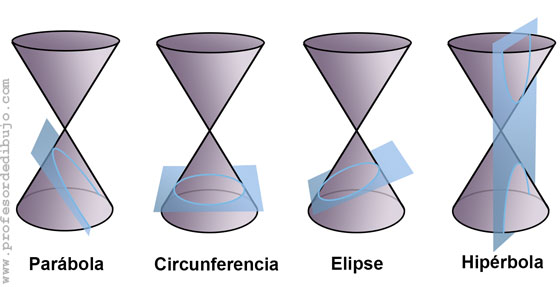
Se distinguen cuatro tipos:

• Circunferencia: si el plano secante es perpendicular al eje de la superficie de revolución, la curva obtenida será una circunferencia.
• Elipse: si el plano secante es oblicuo al eje y corta a todas las generatrices del cono, la curva resultante es una elipse.
• Parábola: si el plano secante es paralelo a una de las generatrices del cono, la curva obtenida será una parábola.
• Hipérbola: si el plano secante es paralelo al eje de la superficie de revolución, la curva resultante será una hipérbola. En este caso corta a dos ramas de la superficie de revolución.

Definición y elementos de la elipse.

Es una curva plana, cerrada y con dos ejes de simetría cuyos puntos cumplen la condición de que la suma de distancias a dos interiores llamados focos es constante. El valor de dicha suma es igual a la del diámetro mayor, conocido como 2a.

• Eje mayor: se llama también eje real o diámetro mayor y se representa como 2a. La suma de distancias de un punto cualquiera de la elipse a ambos focos es igual a su longitud.
• Eje menor: es perpendicular al eje mayor en su punto medio O y se representa como 2b. Recibe también el nombre de eje imaginario.
• Focos: Son dos puntos fijos de referencia y equidistan del centro O de la elipse.
• Distancia focal: Es la magnitud existente entre los focos y se representa como 2c.
• Radios vectores: Son los segmentos que unen un punto de la elipse con ambos focos. La suma de sus distancias es igual a 2a (diámetro mayor).
• Circunferencia principal: Tiene como centro el de la elipse y su diámetro es 2a. De modo que pasa por los extremos del eje mayor de la elipse. Existe una afinidad entre esta circunferencia y la elipse cuyo eje es el diámetro mayor. La dirección de esta afinidad es perpendicular a ese diámetro.
• Circunferencia focal: Es la que tiene como centro uno de los focos y como diámetro 2a (eje mayor). Existen pues dos circunferencias focales.
• Diámetros conjugados: Cualquier segmento que una dos puntos de la elipse pasando por el centro O se considera diámetro. Se llaman diámetros conjugados a todo par de diámetros que cumplen con la condición de que cualquier recta secante a la elipse y paralela a uno de ellos queda dividida en dos partes iguales por el otro. Los ejes de la elipse son los únicos diámetros conjugados que son perpendiculares entre si.
• Excentricidad: La excentricidad de la elipse se define como el cociente entre la semidistancia focal (c) y el semieje mayor (a). La cantidad resultante siempre es menor a la unidad. Cuanto más cerca está el foco del centro de la elipse, más se asemeja la elipse a una circunferencia. Si c es nula la excentricidad es cero y la curva ya no es una elipse, sino una circunferencia. En cambio, si la excentricidad se acerca a uno la elipse se va alargando hasta convertirse en una parábola.

Definición y elementos de la parábola.

La parábola es una curva plana, abierta y simétrica cuyos puntos equidistan de una recta (directriz) y de un punto (foco). Tiene un eje perpendicular a la directriz. La parábola es simétrica respecto a ese eje, en el que están situados tanto el foco como el vértice. El vértice, como punto de la curva que es, equidista del foco y la directriz. Por lo tanto estará situado a la mitad del segmento que une el foco con la directriz.

• Circunferencia principal: es una circunferencia de radio infinito, puesto que es allí donde está el centro de la curva. Queda representada como una recta tangente a la parábola por el vértice.
• Circunferencia focal: Es también una circunferencia de radio infinito. Es por ello que se representa como una recta coincidente con la directriz de la parábola.
• Radios vectores: unen un punto de la curva con el foco y la directriz. Ambos segmentos de unión tienen siempre la misma medida.
• Parámetro: Se conoce como parámetro, tanto en la parábola como en la elipse y la hipérbola, a la longitud de la cuerda perpendicular al eje por el foco. Se representa como 2p. La mitad de esta longitud coincide con la distancia entre el foco y la directriz.

Definición y elementos de la hipérbola.

La hipérbola es una doble curva abierta con dos ejes de simetría cuyos puntos cumplen la condición de que su diferencia de distancias a los focos es una constante conocida como 2a.

• Eje mayor: La diferencia de distancias de un punto cualquiera de la curva a los focos es una medida constante e igual al eje mayor, la distancia entre los vértices, conocido también como eje real y se representa como 2a.
• Eje menor: se representa como 2b, es perpendicular al eje mayor en su punto medio. Su medida se obtiene del triángulo rectángulo que posee como un cateto la distancia a y como hipotenusa la distancia c. Conocido también como eje imaginario.
• Focos: son dos puntos de referencia situados en el eje mayor que equidistan del centro de la hipérbola.
• Distancia focal: es la distancia existente entre los dos focos y se representa como 2c.
• Radios vectores: son los segmentos que unen cada uno de los puntos de la hipérbola con los focos.
• Circunferencia principal: es aquella que tiene como centro el de la hipérbola y como radio a.
• Circunferencia focal: es aquella que tiene como centro uno de los focos y como radio 2a. Puesto que la hipérbola tiene dos focos también tiene dos circunferencias focales.
• Asíntotas: son las dos rectas tangentes a la curva en los puntos situados en el infinito. Pasan por el centro de la hipérbola y son simétricas entre sí.