Índice de Contenidos
Ángulos aplicados a la circunferencia.
Ángulo entre dos circunferencias.
El ángulo de dos circunferencias es el ángulo formado por dos tangentes de una y otra en un punto común a ambas circunferencias. La unión de dicho punto con los centros de ambas circunferencias produce un ángulo suplementario del anterior.
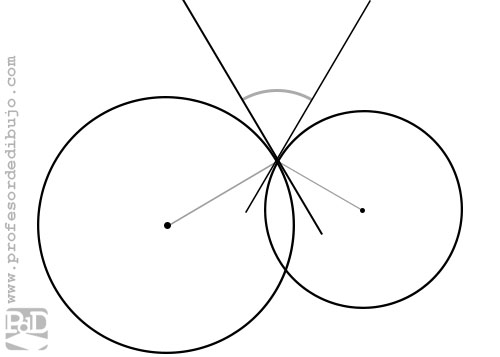
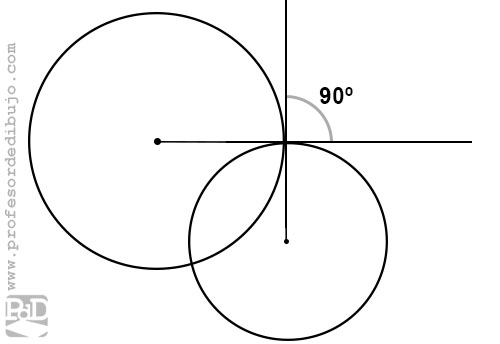
Se llaman circunferencias ortogonales a aquellas que se cortan formando un ángulo perpendicular.
Para el desarrollo de los siguientes contenidos es importante que tengamos presentes algunos conceptos básicos:
- La suma de ángulos consecutivos alrededor de un punto es 360º.
- La suma de ángulos consecutivos a un lado de una recta es 180º.
- La suma de ángulos interiores de un triángulo es 180º
Ángulo central.
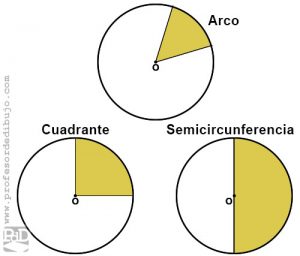
Se denomina ángulo central a aquel que tiene su vértice en el centro de la circunferencia. El conjunto de puntos de la circunferencia comprendidos entre los lados del ángulo se llama arco.
Arcos destacados son:
- Cuadrante: cuando el ángulo central que lo produce mide 90º.
- Semicircunferencia: cuando el ángulo central que lo produce mide 180º.
Ángulo inscrito.
Se llama ángulo inscrito en una circunferencia al que tiene su vértice en un punto de ella y sus lados son cuerdas de la misma. El ángulo inscrito siempre mide la mitad que el ángulo central definido por los cortes de las cuerdas en la circunferencia.
A continuación veremos algunos ejemplos con distintos tipos de ángulos inscritos.
El primer caso es un ángulo inscrito con uno de sus lados pasando por el centro de la circunferencia. Por lo tanto, una de sus cuerdas es un diámetro.
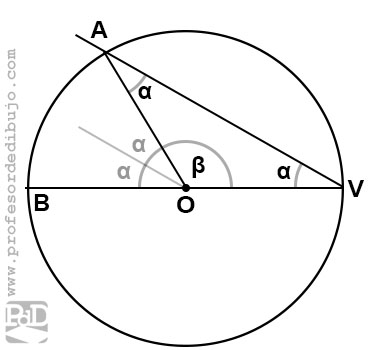
Tenemos el ángulo inscrito AVB (α).
Si nos fijamos, veremos que el triángulo AOV es un triángulo isósceles puesto que los lados AO y VO son dos radios de la circunferencia.
De modo que los ángulos A y V son iguales, son α (alfa). El otro ángulo del triángulo, sitiado en el centro, lo llamaremos beta.
De lo que se deduce que 2α + beta = 180º, ya que estos son los tres ángulos del triángulo AOV.
Por otro lado vemos que AOB es el central definido por los corte de los lados del angulo inscrito V. AOB también es adyacente de beta y por tanto AOB más beta tambien suma 180º puesto que son suplementarios.
En definitiva, teniendo en cuenta que:
2α + beta = 180º
AOB + beta = 180
Se deduce que 2α = AOB. Con esto queda demostrado que el ángulo inscrito (alfa) mide siempre la mitad del ángulo central (AOB) definido por los puntos de corte de las cuerdas del ángulo inscrito.
En este segundo caso tenemos un ángulo inscrito en el que el ambas cuerdas rodean el centro y este es un punto interior al ángulo.
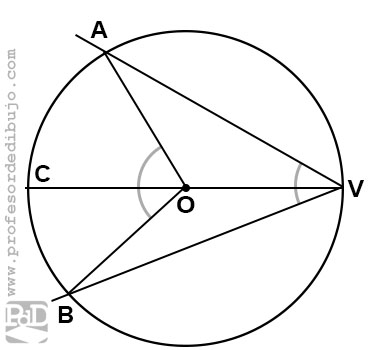
Como vemos, en este caso el ángulo AVB es un ángulo inscrito que comprende al centro.
Si analizamos el ángulo nos daremos cuenta que en este caso tenemos dos veces el caso anterior. Podemos descomponer el ángulo trazando un diámetro que tenga como uno de sus extremos el vértice V. De este modo obtenemos los ángulos AVC y CVB. Ambos ángulos responden al tipo de ángulo inscrito visto en el caso anterior. Su medida será la mitad de sus respectivos interiores.
También debemos tener presente que el ángulo AVB es igual a la suma de AVC y CVB.
De modo que si el ángulo AVB es igual a la suma estos dos. La medida del angulo AVB será la mitad de la suma de sus respectivos ángulos centrales. Esta suma no es otra que AOB, su propio ángulo central definido por los puntos de corte de las cuerdas del ángulo inscrito.
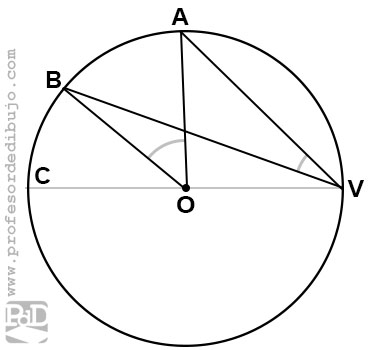
El tercer caso de ángulo inscrito será un ángulo que no comprenda al centro de la circunferencia.
Si lo analizamos, podemos tomar este ángulo AVB como el resultado de la resta de dos ángulos inscritos con un lado pasando por el centro; el primer caso que hemos visto.
AVB = AVC – BVC
Ambos ángulos miden la mitad que sus centrales. De modo que AVC es igual a AOC/2 y BVC es igual a BOC/2.
Podemos decir que el ángulo AVB mide la diferencia sus respectivos centrales: AVB = AOC/2 – BOC/2 = AOB/2. Es decir, la mitad del ángulo central AOB definido por los cortes de las cuerdas del ángulo inscrito AVB.
Ángulo seminscrito.
Se llama ángulo seminscrito en una circunferencia al que tiene el vértice en ella y como lados una cuerda y la tangente a la circunferencia por el vértice. El valor del ángulo seminscrito es también la mitad del ángulo central correspondiente.
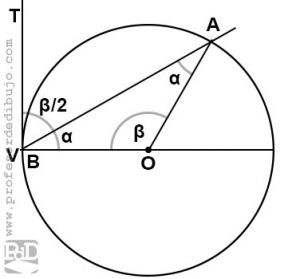
Tenemos el ángulo seminscrito TVA, donde T es la tangente a la circunferencia. Su ángulo central correspondiente sería VOA (β).
Si consideramos el triángulo isósceles VOA veremos que beta + 2α = 180º. Y por lo tanto β/2 + α es igual a 90º. El ańgulo complementario de α sería β/2.
β + 2α = 180º / β/2 + α = 90º
Por otro lado vemos que nuestro ángulo seminscrito + α da como resultado un ángulo recto TVO. Esto quiere decir que nuestro ángulo seminscrito es el complementario del ángulo α, que como vimos anteriormente es beta/2.
De este modo queda demostrado, que al igual que en los ángulos inscritos, el ángulo seminscrito también es la mitad del ángulo central correspondiente.
Ángulo exterior.
Se denomina ángulo exterior a una circunferencia a aquel que, teniendo como vértice V un punto exterior a la circunferencia, sus lados cortan a la circunferencia. Sus dos lados secantes a la circunferencia generan cuatro puntos de corte que llamaremos A, A’, B y B’.
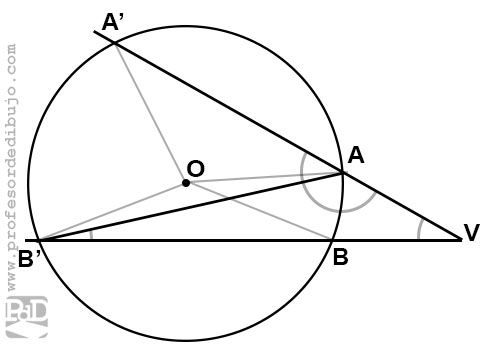
La medida de un ángulo exterior es la semidiferencia entre los dos ángulos centrales correspondientes a los dos arcos interiores (AB y A’B’) determinados por los puntos de corte de los lados del ángulo sobre la circunferencia.
Para razonar esta conclusión trazaremos una cuerda auxiliar AB’ y consideraremos el triángulo AB’V. Como ya sabemos la suma de los ángulos de un triángulo es 180º:
180º = B’AV+AVB’+VB’A
Podemos decir que:
180º – B’AV = AVB’+VB’A
El ángulo de triángulo B’AV es también el suplementario de A’AB, por tanto’: B’AV+A’AB’ = 180º
O lo que es lo mismo: 180º – B’AV = A’AB’
Teniendo en cuenta la conclusión de ambas ecuaciones podemos concluir que A’AB’ = AVB’+VB’A. O lo que es lo mismo, el ángulo exterior AVB’ = A’AB’ – VB’A, donde estos dos últimos, como vemos, son los ángulos inscritos correspondientes a los arcos interiores a los lados del ángulo.
Ángulo interior.
Se llama ángulo interior a una circunferencia a aquel que tiene su vértice dentro de ella. Su valor es la mitad de la suma de los ángulos centrales correspondientes a los arcos determinados por el ángulo interior y su opuesto.
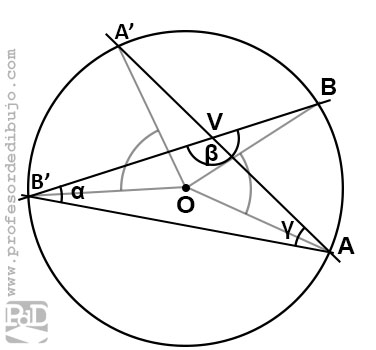
Para su demostración deberemos tener en cuenta que el ángulo interior BVA (En adelante V) es complementario de beta. Por lo tanto:
β + V = 180º / V = 180º – β
Por otro lado deberemos considerar el triángulo B’AV y en concreto la suma de todos sus ángulos:
α + β + γ = 180º /
α + γ = 180º -β
De lo cual se deduce:
V = α + γ
Y puesto que estos son ángulos inscritos que tienen como valor la mitad de sus ángulos centrales. Se deduce que V será la semisuma de sus ángulos centrales.
