Distintos casos de transformaciones geométricas explicadas en vídeo: transporte por varios métodos, traslación, giro, simetría axial, semejanza, equivalencia…
Índice de Contenidos
Transformaciones isométricas.
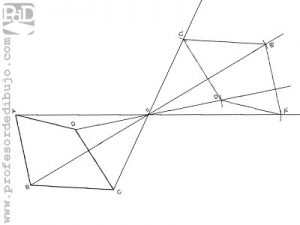
Transporte o copia de polígonos.
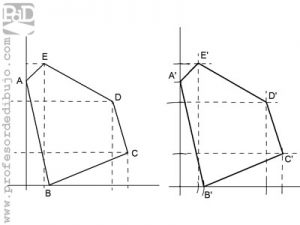
Trazar un polígono igual a otro mediante coordenadas.

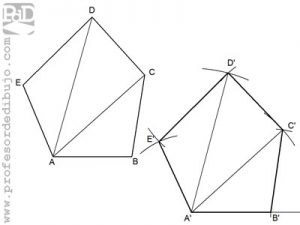
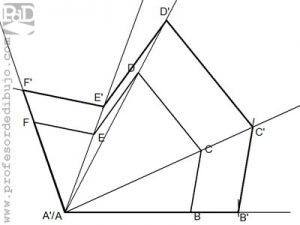
Trazar un polígono igual a otro mediante triangulación.

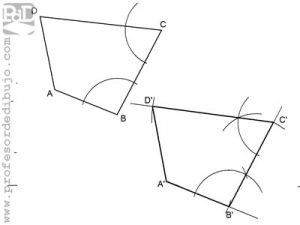
Trazar un polígono igual a otro mediante transporte de ángulos.

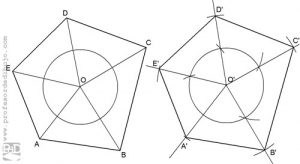
Trazar un polígono igual a otro por radiación.

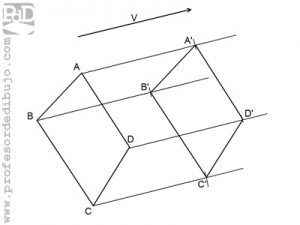
Traslación.
Giro
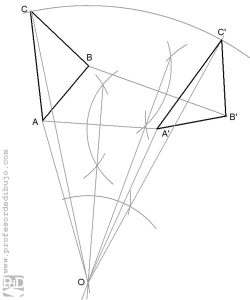
Giro de un polígono en sentido dextrógiro ( 120 º en sentido horario, positivo).

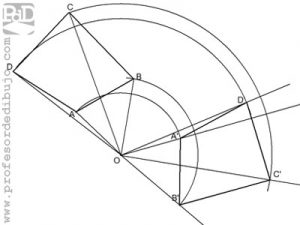
Hallar el centro de giro para girar un polígono.

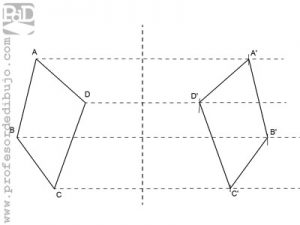
Simetría.
Transformaciones isomórficas.
Semejanza.
Transformaciones anamórficas.
Equivalencia.
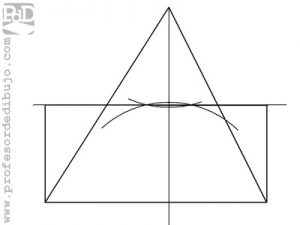
Trazar un rectángulo equivalente a un triángulo dado.

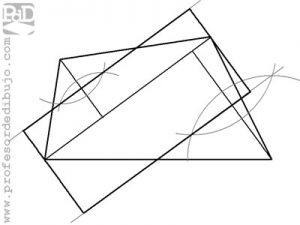
Trazar un rectángulo equivalente a un cuadrilátero dado.

Apéndice teórico.
Introducción a Transformaciones geométricas.
Una transformación geométrica es una operación en la que partiendo de una figura dada obtenemos una nueva. En la transformación existe una correspondencia entre ambas figuras y sus elementos.
Los movimientos son transformaciones geométricas en las que la figura conserva la forma y el tamaño de su correspondiente figura inicial.
Clasificación de las transformaciones geométricas.
Basándonos en como afecta la transformación a las características métricas y formales de la figura final respecto a la inicial, podemos clasificar estas transformaciones en tres grupos:
- Transformaciones isométricas. Son transformaciones caracterizadas porque la figura resultante las medidas y los ángulos de la figura inicial. Mantiene la forma y el tamaño, resultando una figura igual a la inicial. Las transformaciones pertenecientes a este tipo coinciden con los llamados movimientos: traslación, giro, identidad y simetría.
- Transformaciones isomórficas. Son aquellas en las que la figura resultante conserva la forma de la figura inicial, pero varía el tamaño. Es decir, los ángulos se conservan y las magnitudes son distintas, pero proporcionales. En este grupo nos encontramos con la homotecia, la semejanza y las escalas.
- Transformaciones anamórficas. Son transformaciones en la que la figura resultante es completamente diferente a la inicial. Varían forma y magnitud y sólo mantiene alguna propiedad derivada de la figura original. En este grupo estarían equivalencia, homología e inversión.
Identidad e igualdad.
Antes de abordar cada una de las transformaciones sería conveniente aclarar la diferencia entre estos dos términos.
Decimos que dos figuras son iguales cuando sus lados y sus ángulos son iguales y están dispuestos en el mismo orden. Sin embargo, pueden mantener este orden y estar dispuesta en sentido contrario.
En cambio, dos figuras son idénticas si sus ángulos, lados, disposición de elementos y sentido son iguales. Esto nos permitiría superponer una figura sobre la otra y coincidirían exactamente.
La identidad, por tanto, no afecta a ningún atributo de la figura. Esta permanece invariable. En cambio, en la igualdad varia el sentido en el que se disponen los elementos de la figura. Es por ello que podemos concluir que todas las figuras idénticas son iguales, pero no al contrario.