Índice de Contenidos
Perspectividad entre dos planos.
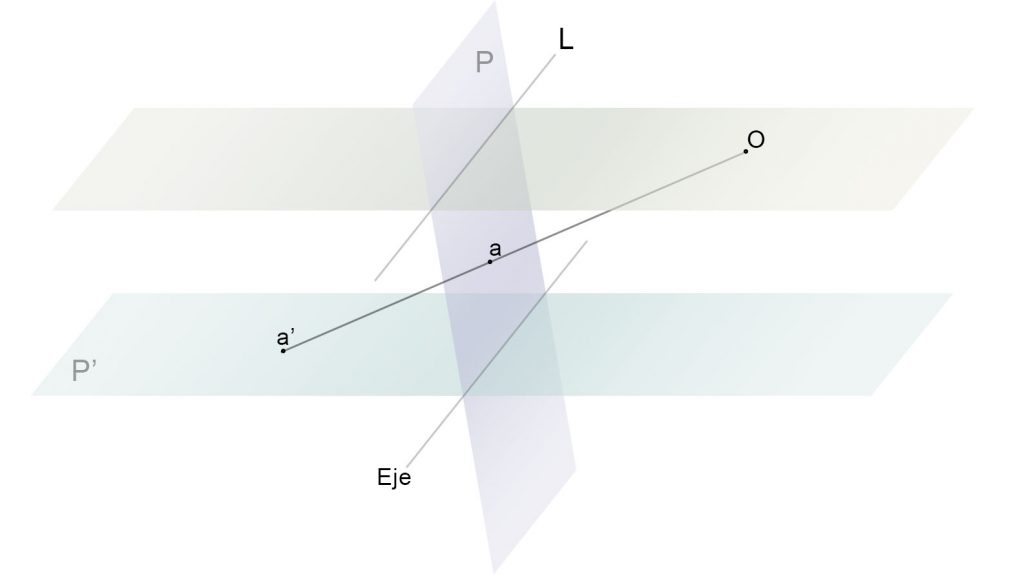
Dados dos planos P y P’ y un punto O que no pertenece a ellos, se establece una correspondencia entre los puntos de dichos planos. De la siguiente manera, al punto A del plano P le corresponde el punto A’, el cual hallamos por la intersección de la recta OA con el plano P’.
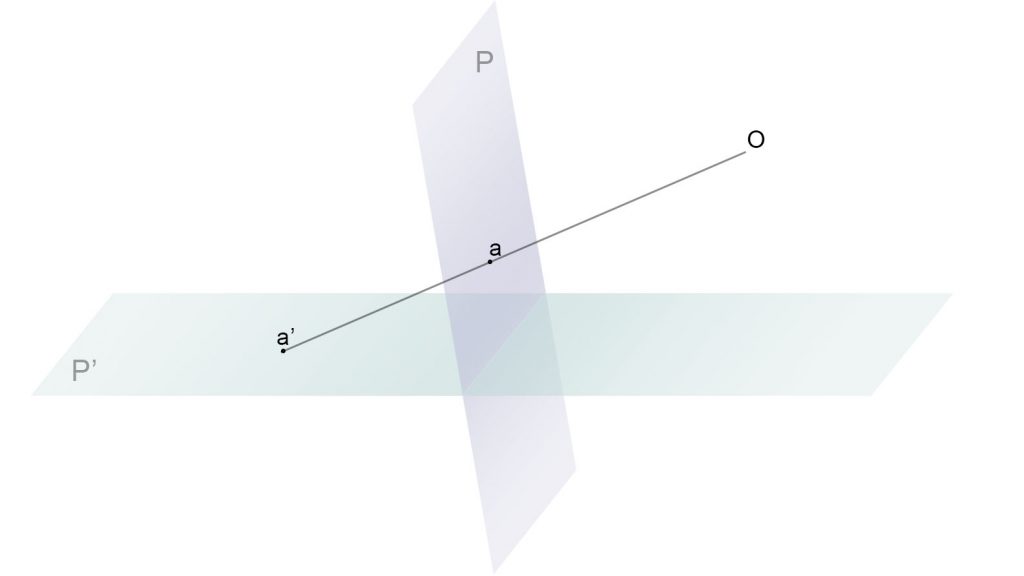
Esta correspondencia establece la perspectividad entre planos. A y A’ son puntos homólogos.
Los homólogos de los puntos impropios, del infinito, del plano P’ son los puntos de la recta límite L. De igual manera los homólogos de la recta L’ son puntos que están en el infinito del plano P. La recta E es la intersección entre ambos planos P y P’.

Como propiedades de esta correspondencia:
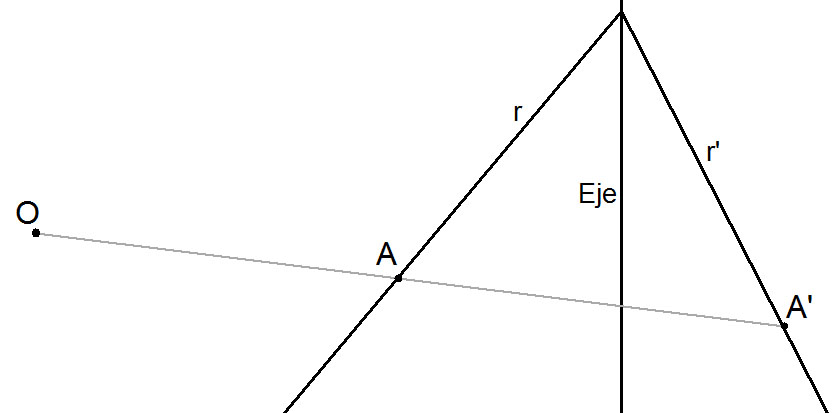
- Dos puntos homólogos están alineados con el origen o centro de la radiación O.

- La recta E, considerada eje, es doble. Esto significa que es homóloga de sí misma.
- Una recta que corta al eje se corta en ese mismo punto con su recta homóloga.

Homología.
Una homología es una transformación geométrica homográfica que relaciona dos formas planas, generadas por sección , pertenecientes a una misma radiación. Es una transformación proyectiva tridimensional, pero al tratarse de una homografía es posible su resolución plana abatimiento de los planos y proyección. Esta circunstancia será la base de los para el desarrollo gráfico de los sistemas de representación.
Como se ha comentado antes, será necesario abatir en un mismo plano de representación los dos planos que conforman la homología. Este abatimiento se puede hacer uno sobre otro, quedando ambos planos a un lado del eje o abatiéndolos cada plano a un lado del eje.
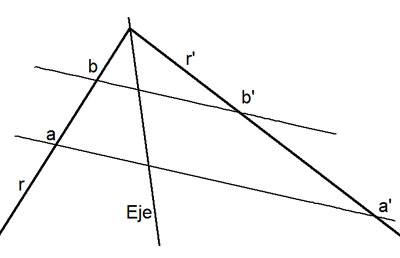
Para que dos figuras sean homológicas deberán cumplir dos condiciones. Son las mínimas exigibles para que podamos considerar una relación homológica entre figuras:
- Un par de puntos homólogos alineados con el punto O, centro de la homología.
- Un par de rectas homólogas que se corten en un punto del eje de la homología.
Como ya vimos, son puntos dobles todos aquellos que sean homólogos de sí mismos. Todos los puntos dobles de una homología están situados en el eje.
Afinidad (Homología afín).
Si el origen de la radiación de una homología está situado en el infinito, estamos ante un tipo de homología conocida como afinidad u homología afín. Las rectas de la radiación que pasan por puntos homólogos son paralelas entre sí, tienen todas una misma dirección. Y al encontrarse el centro de la radiación en el infinito, las rectas límite también estarán en él. Esto supone que a efectos prácticos las rectas límites de una afinidad no aparezcan el el trazado.
Se cumplen las siguientes condiciones:
- Los puntos homólogos están alineados en base a la dirección de la afinidad.

- Un par de rectas homólogas de una afinidad, al igual que en la homología, se cortan en el eje.

Rectas límites.
Es el momento de analizar que son las rectas límite y profundizar en el aspecto tridimensional que tiene la homología y que muchas veces se obvia.

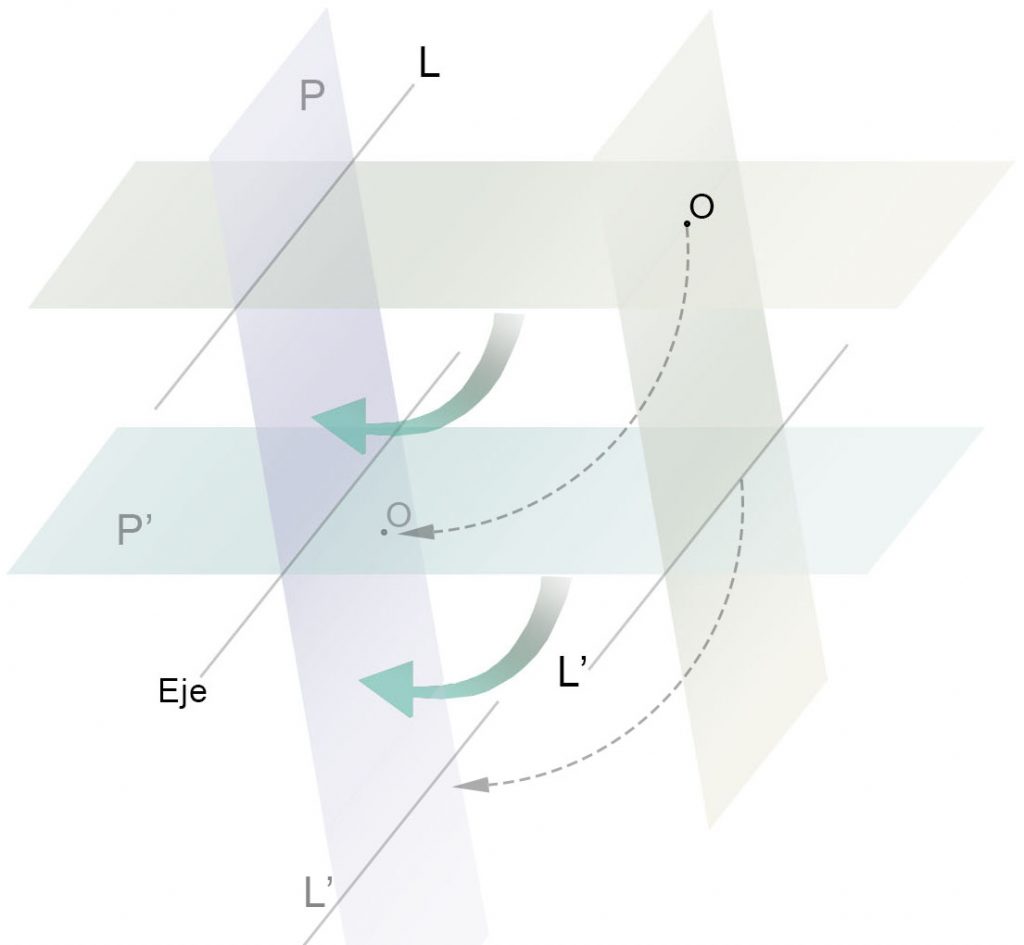
Si tomamos cada vez puntos del plano P’ más alejados del eje veremos que sus homólogos también se alejan de este y las rectas de radiación cada vez se aproximan más a ser una paralela a dicho plano P’.
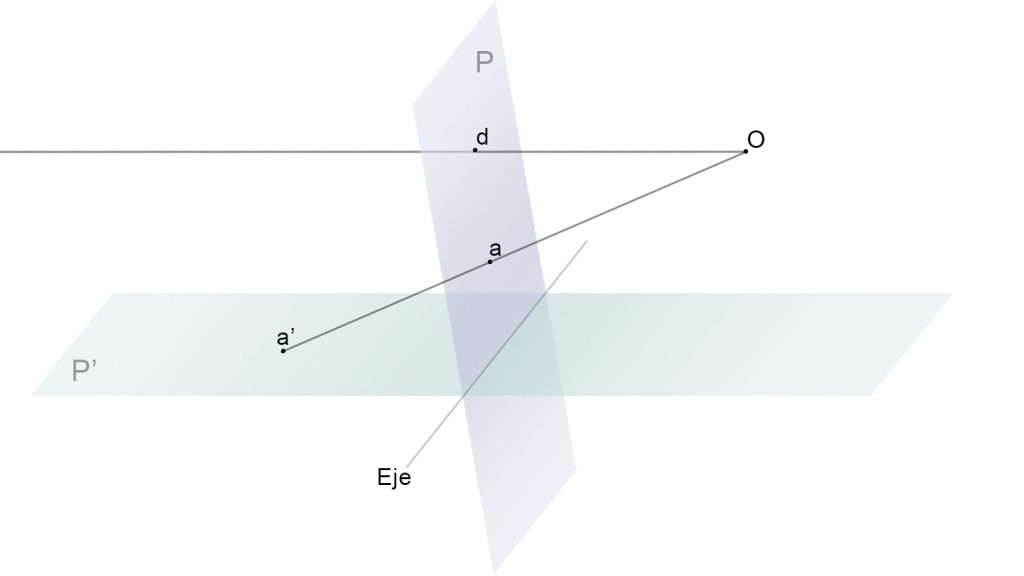
Si tomáramos un punto d’ impropio, del infinito, del plano P’ su recta de unión al centro de radiación sería paralela al plano y su punto homólogo d en plano P estaría a la misma altura (respecto a P’) que el centro de radiación.
Con lo cual, si trazamos por el centro de radiación un plano paralelo al plano P’ estaríamos conteniendo en él todas las rectas de radiación para los puntos situados en el infinito del plano P’. La intersección del plano paralelo a P’ con el plano P produciría la recta límite L donde estarían todos los puntos homólogos a los puntos impropios del plano P’.

Igual sucedería si trazamos un plano paralelo al plano P que pase por el centro de radiación. Obtendríamos la recta límite L’ donde están los homólogos en el plano P’ todos los puntos del plano P situados en el infinito.
De tal modo que las rectas límites de una homología son el lugar geométrico de todos los puntos homólogos de los situados en el infinito del otro plano.
Como están generadas por un sistema de planos paralelos dos a dos, la distancia de una de ellas al eje es la misma que la distancia de la otra al centro de radiación, y viceversa. Y es por este motivo también que las rectas límite serán paralelas al eje. Ambas propiedades se mantendrán cuando el sistema este abatido y representado en el plano.
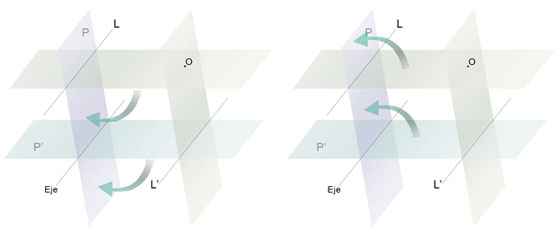
Existirían dos posibilidades a la hora de abatir los planos para su representación. En función de como se haga las rectas límite quedarán las dos entre el centro de la homología y el eje, o ambas por fuera.
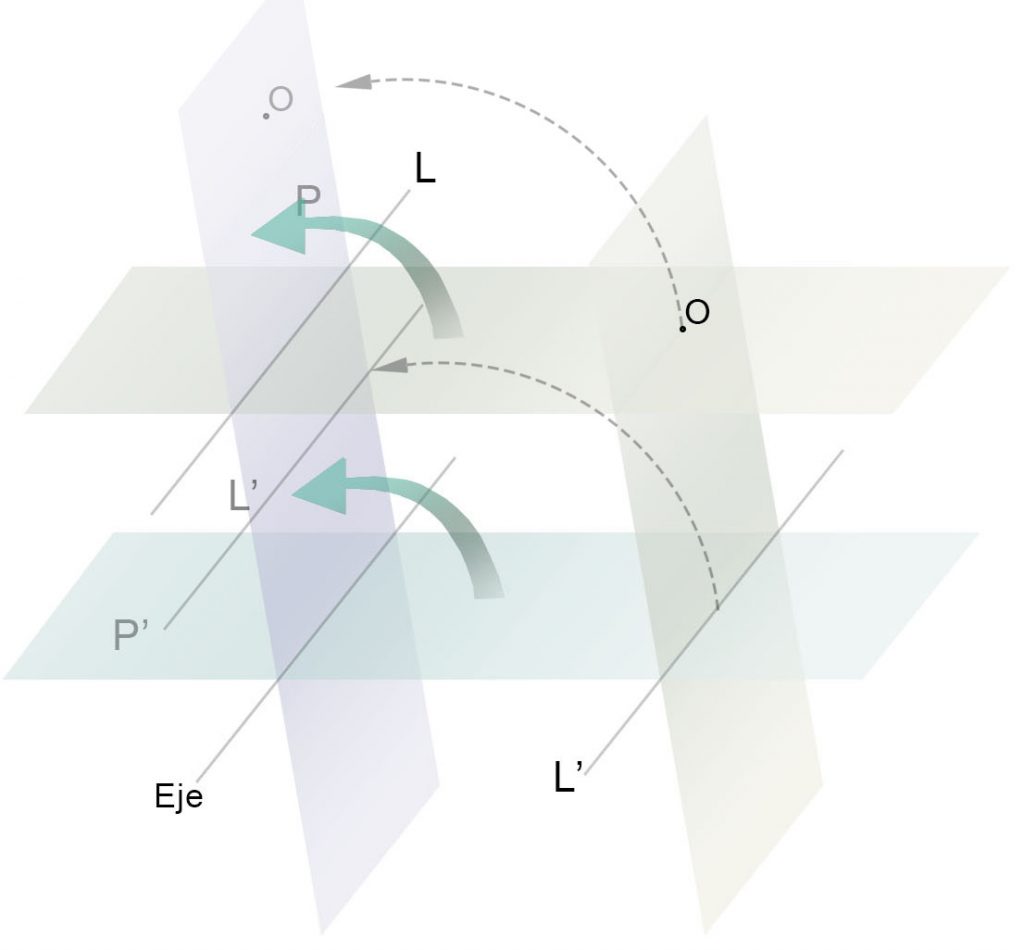
Para hallar las rectas límite de una homología basta con tener en cuenta otra propiedad: Todas las rectas de un plano que se cortan en un punto de su correspondiente recta límite, sus homólogas son paralelas a la dirección del segmento que une dicho punto con el centro de la radiación.