En este apartado repasaremos los conceptos y trazados más elementales. Son contenidos que se desarrollaron en Educación Plástica y Visual durante la Secundaria Obligatoria. Es fundamental que el alumno tenga asimilados todo estos conceptos para que el presente curso se desarrolle con naturalidad.
Índice de Contenidos
Elementos geométricos básicos.
- Punto: Mínima unidad geométrica. No tiene longitud, ni profundidad, ni anchura. Esto quiere decir que un punto simplemente designa una posición. Se nombran con letra mayúscula y se puede representar con distintos convencionalismos. Los más habituales son un pequeño círculo, un punto y una pequeña cruz en forma de X o aspa. Podemos distinguir dos tipos de puntos:
- Punto propio: es aquel que está situado en el espacio y se puede representar.
- Punto impropio: es aquel que está situado en el infinito, fuera del plano, y por lo tanto no se puede representar.
- Línea: Se define como una sucesión de puntos. No tiene ni principio ni fin. Se puede distinguir dos tipos:
- Línea recta: sucesión de puntos con una dirección fija. Para nombrarlas se les asigna una letra minúscula. Las rectas, según su posición se pueden clasificar en: vertical, horizontal e inclinada.
- Línea curva: sucesión de puntos con una dirección variable. Se pueden clasificar como abiertas, cerradas u onduladas.
Relación entre punto y recta.
Un punto respecto a una recta tiene dos posibles posiciones:
- Pertenecer a la recta.
- Estar fuera de ella.
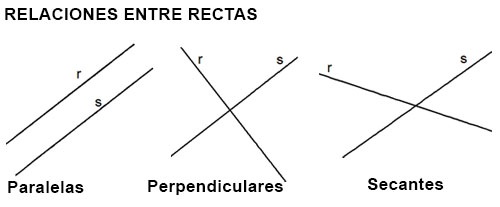
Relaciones entre rectas.
Dos o más rectas pueden relacionarse entre si según sus posiciones:
- PARALELAS: Se dice que dos rectas son paralelas si siempre se mantienen a una misma distancia entre si, y nunca se llegan a cortar.
- PERPENDICULARES: Se dice que dos rectas son perpendiculares cuando al cortarse forman 4 ángulos rectos (90 grados).
- SECANTES: Dos rectas son secantes cuando al se cortan formando ángulos distintos al ángulo recto.
Conceptos generales del dibujo técnico.
Antes de continuar, es importante que dejemos claros algunos conceptos generales.
- Medir: En geometría medir un segmento es determinar el número de unidades que están contenidas en dicho segmento.
- Valor de la medida: Es el número que expresa la medida.
- Distancia: Es el camino más corto que hay entre dos elementos geométricos.
- Equidistancia: Es la igualdad de distancias entre dos o más elementos geométricos.
Distancias:
- Distancia entre dos puntos.
La distancia entre dos puntos viene determinada por la longitud del segmento que los une. - Distancia entre punto y recta.
Se obtiene trazando por el punto una recta perpendicular a la recta dada hasta su intersección con ella. - Distancia entre dos rectas paralelas.
Es la medida de cualquiera de los segmentos que une ambas rectas de forma perpendicular.
El siguiente vídeo enfoca todo lo anteriormente visto para alumnos de primer curso de Educación Plástica en la ESO.
Lugar geométrico: es el conjunto de puntos que cumplen una misma condición. Existen una gran diversidad de lugares geométricos. Serán fundamentales para la resolución de muchos problemas de geometría. A continuación veremos algunos ejemplos básicos que son trazados estudiados en Plástica durante la ESO:
- Mediatriz: es el lugar geométrico de todos los puntos que están a la misma distancia de los extremos de un segmento.
- Bisectriz: es el lugar geométrico de todos los puntos que están a la misma distancia de los lados de un ángulo.
- Circunferencia: es el lugar geométrico de todos los puntos que están a la misma distancia de otro punto llamado centro.
Ángulos.
Se define ángulo como la porción del plano delimitada por dos rectas que se cortan en un punto llamado vértice. Los lados de dicho ángulo serán las propias rectas.
Para medir la amplitud de los ángulos usaremos grados sexagesimales. Como herramienta para dichas mediciones emplearemos un transportador de ángulos.
Según el tipo de líneas que forma el ángulo podemos distinguir tres tipos de ángulos:
- Rectilíneos: son aquellos que están formados por dos rectas.
- Curvilíneos: son aquellos formados por dos arcos de circunferencia.
- Mixtilíneos: son aquellos formados por una recta y una curva.

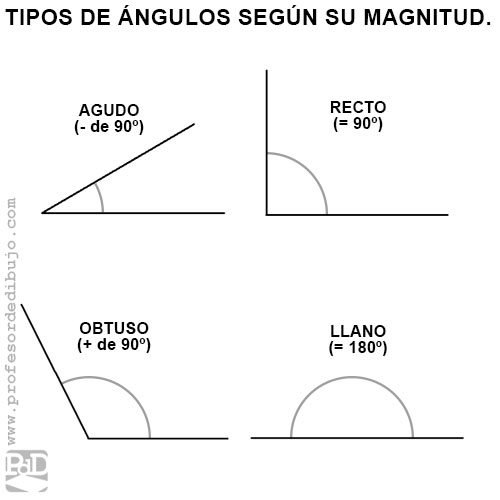
Podemos clasificar los ángulos según su medida:
- Agudo: cuando miden menos de 90º.
- Recto: cuando miden 90º.
- Obtuso: cuando miden más de 90º, pero menos de 180º.
- Llano: cuando miden 180º.
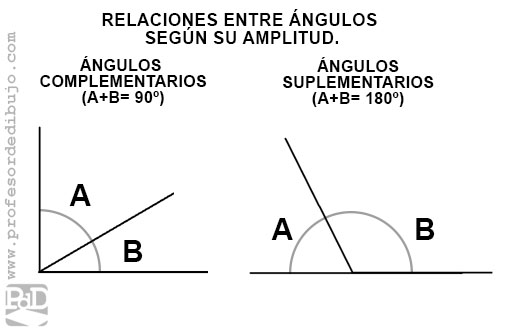
Relaciones entre ángulos según su medida:
Iguales: diremos que dos ángulos son iguales cuando tengan el mismo número de grados, independientemente de su posición.
Complementarios: cuando la suma de ambos ángulos sea 90º.
Suplementarios: cuando sumen 180º.
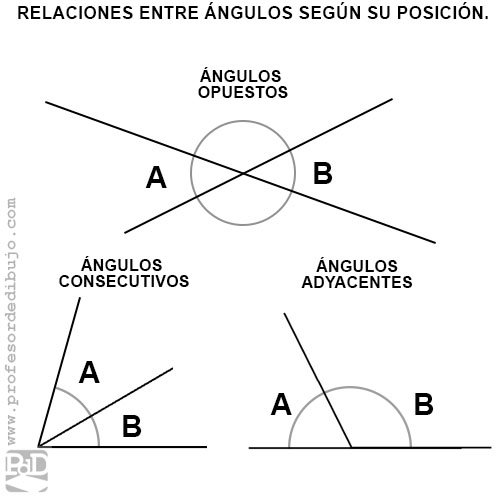
De este modo, según su relación, dos ángulos pueden ser:
- Ángulos opuestos: Son ángulos que tienen un vértice en común y los lados de uno son la prolongación de los lados del otro. Los ángulos opuestos comparten la misma amplitud. Dos rectas que se cortan forman dos pares de ángulos opuestos.
- Ángulos consecutivos: Son ángulos que tienen el vértice y un lado en común.
- Ángulos adyacentes: Son ángulos que tienen el vértice y un lado en común, mientras los otros dos lados son uno la prolongación del otro.