Índice de Contenidos
Definición de polígono.
Un polígono es una figura plana delimitada por una secuencia de segmentos consecutivos no alineados. Dichos segmentos se denominan lados.
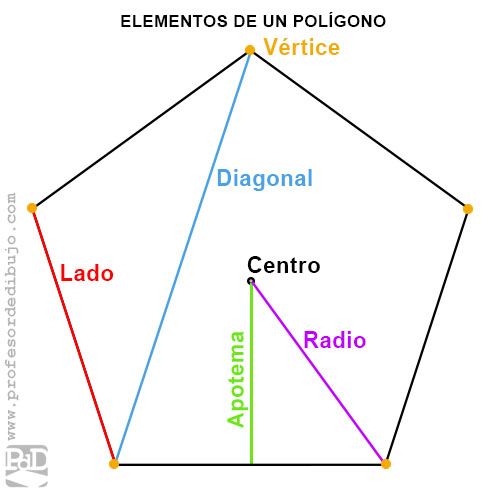
Elementos de un polígono.
- Lado: son los segmentos que forman el polígono. También nombradas como aristas.
- Vértice: es el punto de corte entre dos lados.
- Diagonal: es el segmento que une dos lados no consecutivos.
- Perímetro: es el contorno de la superficie del polígono, la suma de las longitudes de todos sus lados
En polígonos regulares también distinguimos los siguientes elementos:
- Centro: Es un punto equidistante de todos los ángulos y lados.
- Apotema: Es el segmento que une el centro del polígono con el punto medio de cualquiera de sus lados.
- Radio: Es el segmento que une el centro del polígono con cualquiera de sus vértices.
- Ángulo central: es el formado por dos radios que parten del centro a los dos extremos de un mismo lado.


Clasificación de polígonos.
Según su forma:
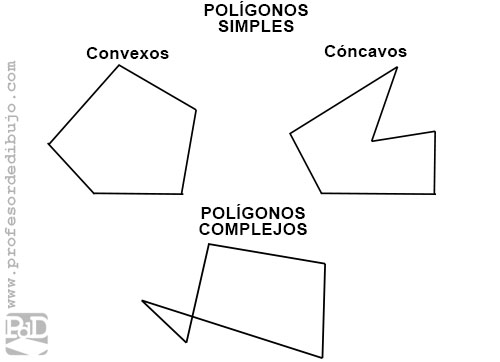
- Simple: Cuando ninguno de sus lados no consecutivos se cortan.
- Convexo: es aquel polígono que tiene todos sus ángulos interiores menores que 180º. Se cumple que al ser atravesado por una recta siempre lo corta en un máximo de dos puntos.
- Cóncavo: es aquel polígono que tiene alguno o varios de sus ángulos interiores menores que 180º. Se cumple que al ser atravesado por una recta puede cortarlo en más de dos puntos.
- Complejo: Cuando dos de sus aristas no consecutivas se cortan.

 Según sus condiciones de regularidad:
Según sus condiciones de regularidad:
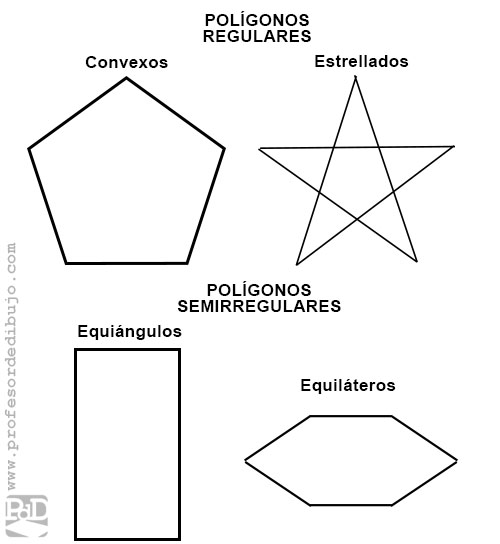
- Regular: son polígonos que tienen todos sus lados y ángulos iguales. Dentro de los regulares encontramos dos tipos:
- Convexos: Son polígonos simples convexos cuyos lados y ángulos son todos iguales.
- Estrellados: Son polígonos regulares cóncavos cruzados con forma de estrella.
- Semirregulares: Son aquellos que tienen todos sus lados o todos sus ángulos iguales, pero no ambos elementos. Distinguimos dos tipos:
- Equiángulo: Son polígonos que tienen todos sus ángulos iguales, pero no sus lados.
- Equilátero: Son polígonos que tienen todos sus lados iguales, pero no sus ángulos.
- Irregular: son aquellos polígonos que tienen lados y ángulos diferentes.


Relaciones del polígono respecto a la circunferencia.
Se contemplan dos tipos de relaciones:
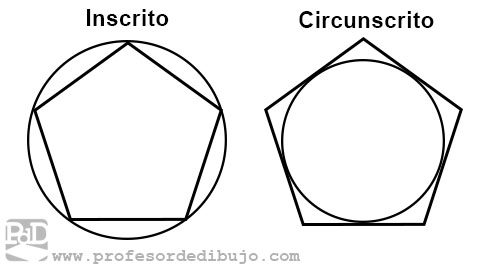
- Inscrito: Se dice que un polígono esta inscrito en una circunferencia cuando todos los vértices del polígono son puntos de dicha circunferencia.
- Circunscrito: Se dice que un polígono está circunscrito a una circunferencia cuando todos los lados del polígono son tangentes a dicha circunferencia.


Polígonos según el número de lados.
| TRIÁNGULO | 3 LADOS |
| CUADRILÁTEROS | 4 LADOS |
| PENTÁGONO | 5 LADOS |
| HEXÁGONO | 6 LADOS |
| HEPTÁGONO | 7 LADOS |
| OCTÓGONO u OCTÁGONO | 8 LADOS |
| ENEÁGONO u NONÁGONO | 9 LADOS |
| DECÁGONO | 10 LADOS |
| ENDECÁGONO | 11 LADOS |
| DODECÁGONO | 12 LADOS |
Nominación.
Los vértices y lados se nombrarán con letras a partir de la «a» y en sentido contrario al de las agujas del reloj. Los ángulos con letras en mayúscula y los lados con la letra del vértice opuesto, pero en minúscula.
Áreas de un polígono.
El área de un polígono es la superficie comprendida dentro de su perímetro. En los polígonos regulares, el área es igual al producto del perímetro por la apotema dividido por dos. En el caso de los polígonos irregulares será necesario recurrir a la triangulación del polígono para calcular su área. Es decir, dividiremos el polígono en triángulos, hallaremos el área de cada uno de ellos y lo sumaremos.
Polígonos estrellados.
Los polígonos estrellados son polígonos regulares cóncavos cruzados con forma de estrella. se obtienen de unir de forma alterna, de dos en dos, de tres en tres…, los vértices de un polígono regular convexo. Debemos distinguir un polígono estrellado de una estrella creada a base de superposición de polígonos. Si cerramos el polígono sin haber pasado por todos sus puntos obtendremos un polígono, pero no estrellado. 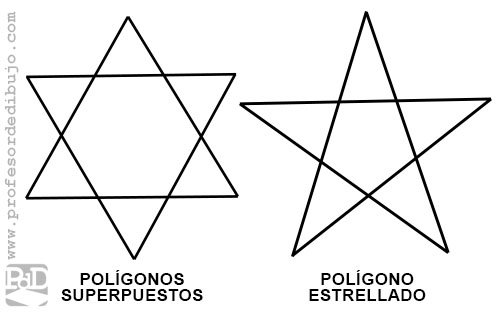

 No se puede sacra polígonos estrellados de todos los polígonos. Y en algunos casos podremos obtener más de un polígono estrellado de un mismo polígono. Propiedades de un polígono estrellado:
No se puede sacra polígonos estrellados de todos los polígonos. Y en algunos casos podremos obtener más de un polígono estrellado de un mismo polígono. Propiedades de un polígono estrellado:
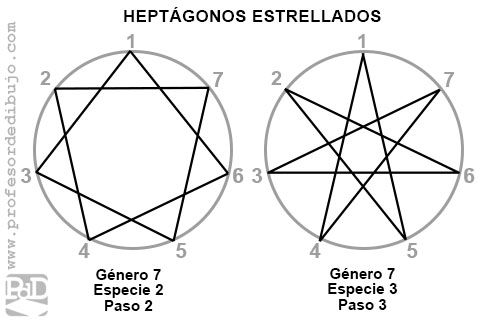
- Género: Es el número de lados que forman el polígono.
- Especie: Es el número de vueltas que debemos dar antes de completar la figura.
- Paso: Es el número de divisiones de la circunferencia que abarca el lado.
- Núcleo: Es el polígono que surge en su interior.
- Nodo: Cada uno de los vértices de un polígono estrellado se denomina nodo.

 Un polígono regular tiene tantos polígonos estrellados como números primos a su número de lados hatyan menores a la mitad de su número de lados. Es decir, si tiene X lados, tiene tantos polígonos estrellados como números primos de X que sean menores de X/2.
Un polígono regular tiene tantos polígonos estrellados como números primos a su número de lados hatyan menores a la mitad de su número de lados. Es decir, si tiene X lados, tiene tantos polígonos estrellados como números primos de X que sean menores de X/2.
| POLÍGONO | Lados | Estrellados | Paso |
| Triángulo | 3 | 0 | 0 |
| Cuadrado | 4 | 0 | 0 |
| Pentágono | 5 | 1 | 2 |
| Hexágono | 6 | 0 | 0 |
| Heptágono | 7 | 2 | 2, 3 |
| Octógono | 8 | 1 | 3 |
| Eneágono | 9 | 2 | 2, 4 |
| Decágono | 10 | 2 | 3, 4 |
| Endecágono | 11 | 4 | 2, 3, 4, 5 |
| Dodecágono | 12 | 1 | 5 |
